图

相关概念

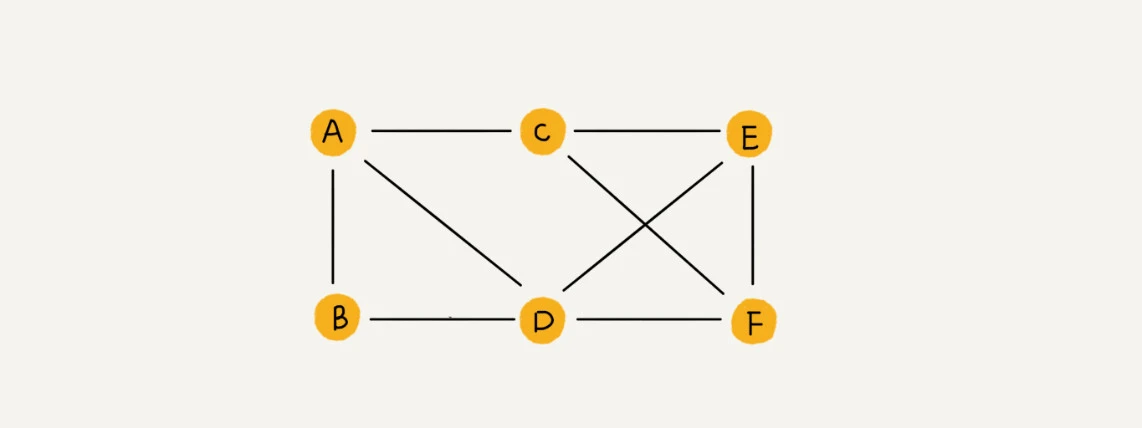
• 图中的元素叫做顶点（vertex）
• 一个顶点可以与任意其他顶点建立连接关系, 这种建立的关系叫做边（edge）
• 顶点相连接的边的条数, 叫做顶点的度（degree）
• 有方向的图叫做“有向图”, 没有方向的图就叫做“无向图”
• 在有向图中，我们把度分为入度（In-degree）和出度（Out-degree）, 顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。
• 在带权图中，每条边都有一个权重（weight）

存储方式

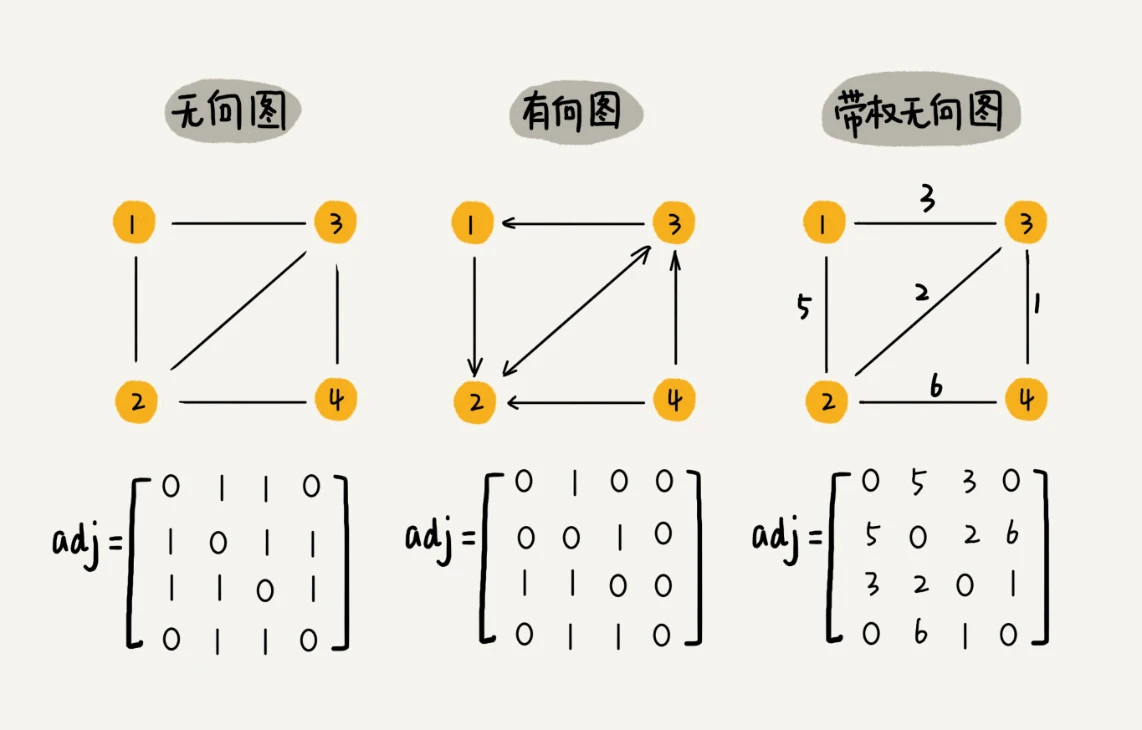
邻接矩阵（Adjacency Matrix）

• 底层为二维数组, 若顶点i与j有边, 则A[i][j]=1, 若为带权图, 则存储相应的权重
• 这个方式简单直观, 获取两个顶点关系时非常高效, 但比较浪费存储空间, 若为无向图, 实际存储一半就醒了, 若为稀疏图的情况, 就是顶点很多但边不多, 比如微信几亿用户, 但好友一般三五百个, 绝大部分的存储空间都会被浪费

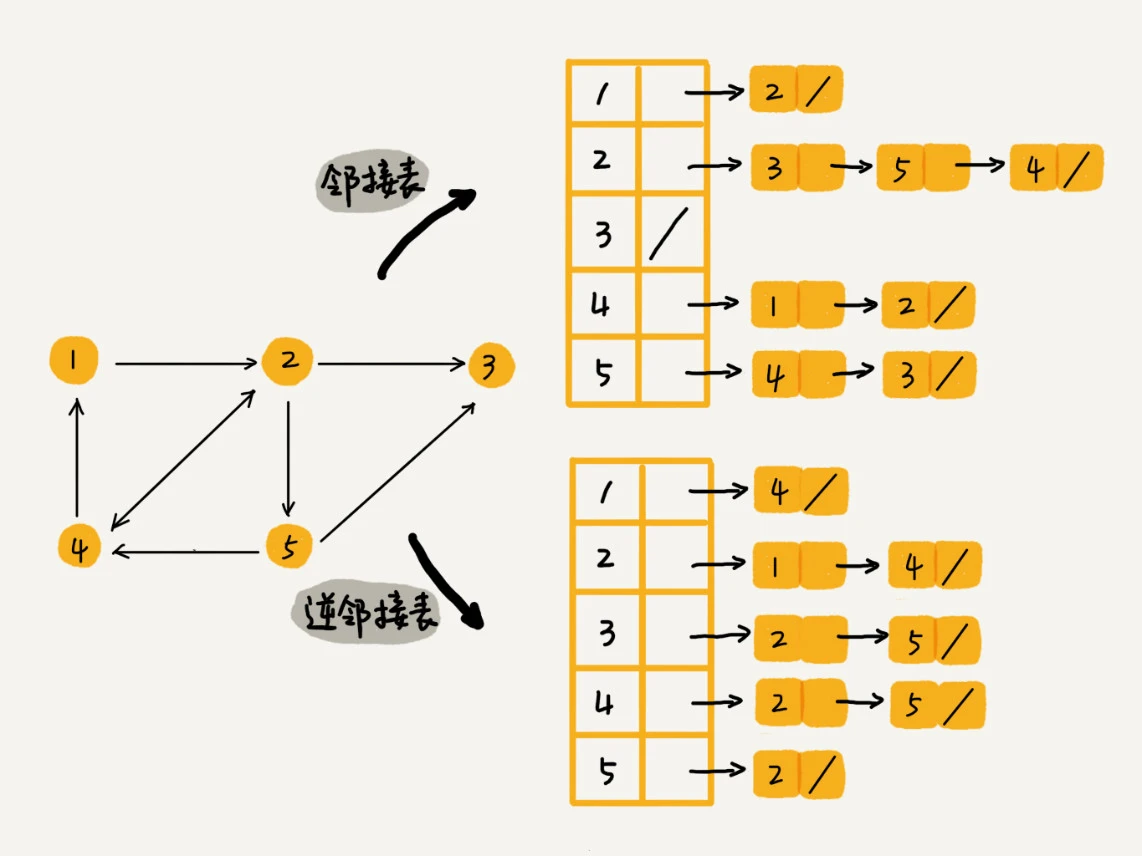
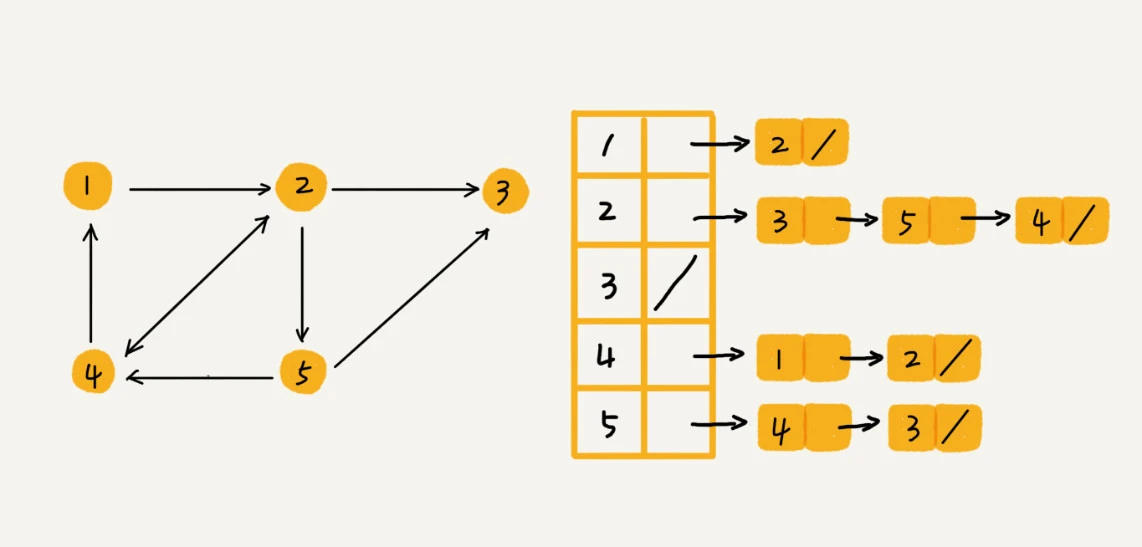
邻接表（Adjacency List）

• 每个顶点对应的链表里面, 存储的是指向的顶点
• 相对于邻接矩阵, 更节省空间, 但查询顶点之间的关系就没那么高效, 为了提高查找效率, 可以将链表换成平衡查找二叉树, 红黑树, 跳表等结构.

应用案例

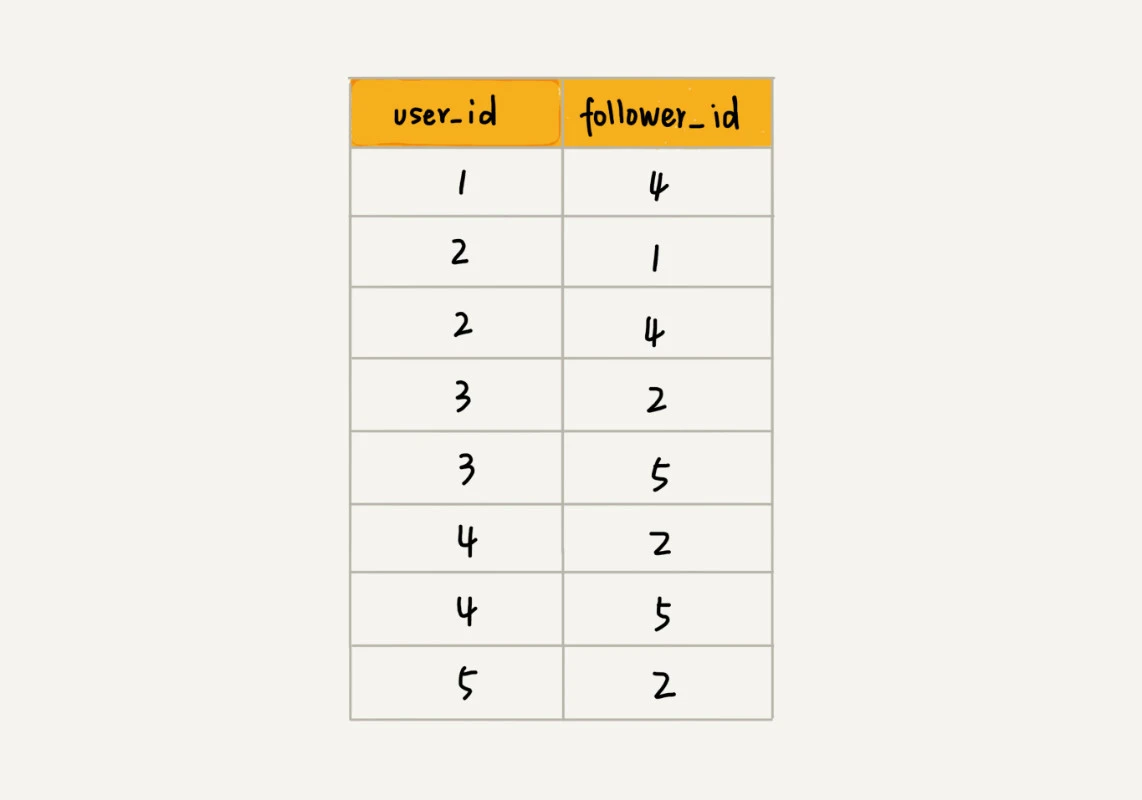
如何存储微博、微信等社交网络中的好友关系？

• 因为社交网络是一张稀疏图, 使用邻接表来存储
• 为了便捷查询粉丝列表, 最好额外维护一张逆邻接表
• 因为需要按照用户名称的首字母排序, 分页获取粉丝或关注的用户列表, 所以最好使用跳表改进邻接表中的链表, 跳表插入、删除、查找都非常高效，时间复杂度是 O(logn)，空间复杂度上稍高，是 O(n)。最重要的一点，跳表中存储的数据本来就是有序的了，分页获取粉丝列表或关注列表，就非常高效。
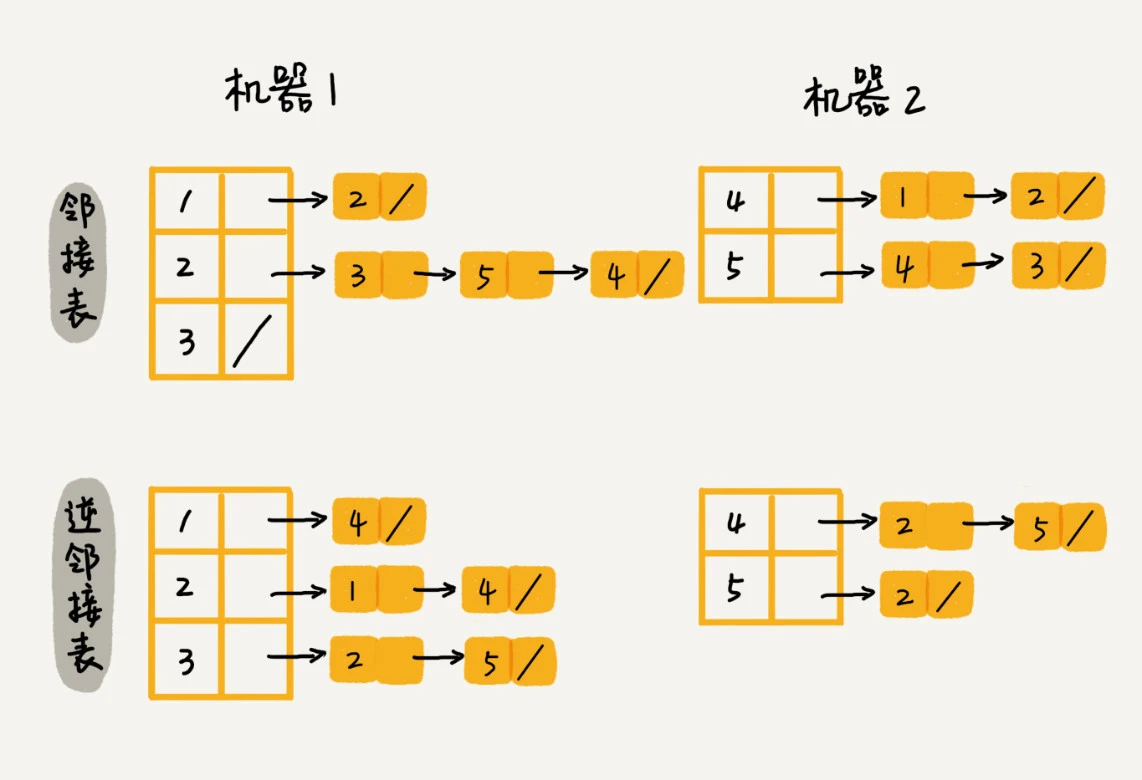
• 如果数据规模过大, 可以使用哈希分片, 将邻接表存储在不同的服务器上, 或是使用数据库存储, 见图三