栈、队列和递归

栈

栈是一种操作受限的线性表，只允许在一端插入和删除数据，特征是后进先出
栈可以用数组或链表实现，可支持动态扩容，入栈push()，出栈pop()时间复杂度都是O(1)，空间复杂度也是O(1)（因为只涉及到单个数据的操作，空间复杂度是指除了原本的数据存储空间，算法运行还需要额外的存储空间）
栈的应用
- 函数调用：操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈
- 表达式求值
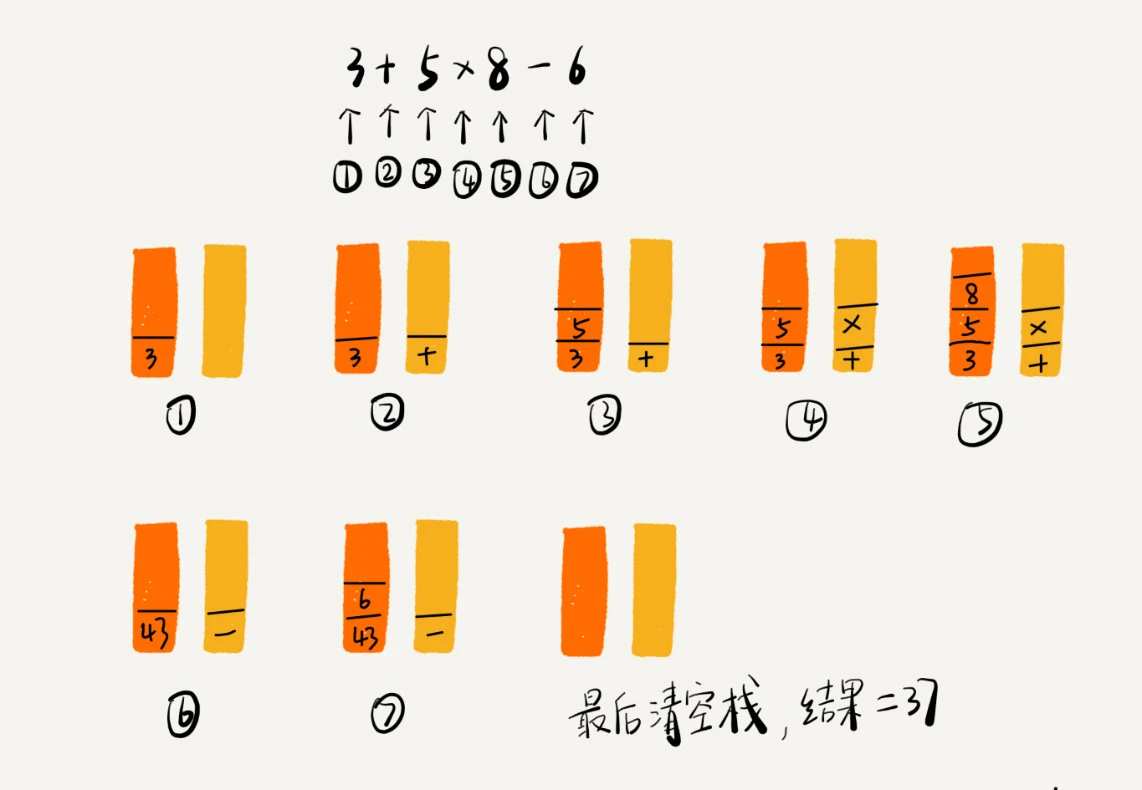
- 括号匹配：栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。
- 实现浏览器前进/后退：使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈 X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。

队列

队列也是一种操作受限的线性表数据结构, 先进先出, 基本操作入队enqueue(), 出队dequeue()
用数组实现的队列叫顺序队列, 用链表实现的队列叫链式队列, 与栈同理

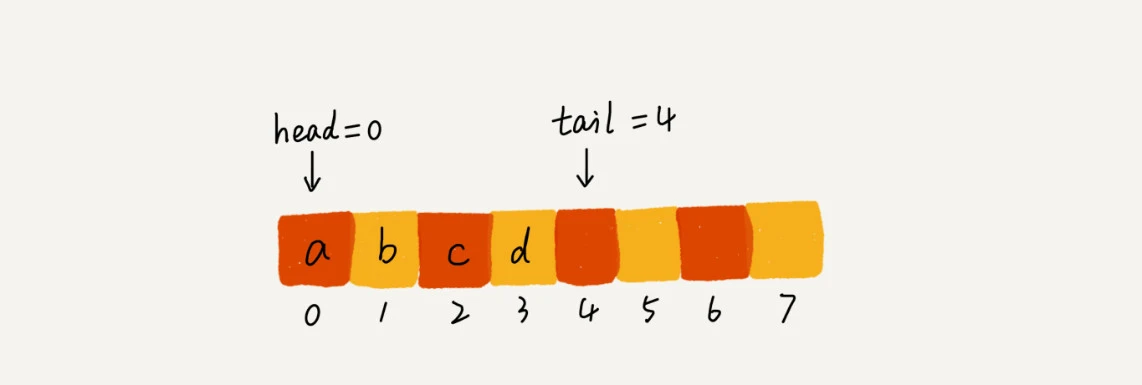
用数组实现的队列

Java

publicclassArrayQueue {
    privateString[] items;
    privateintn = 0;
    privateinthead = 0;
    privateinttail = 0;

    publicArrayQueue(intcapacity) {
        items = newString[capacity];
        this.n = capacity;
    }

    publicbooleanenqueue(String item) {
        if(tail == n) {
            // 队列已满
if(head == 0) {
                returnfalse;
            }

            // 数据搬移
for(inti = head; i < tail; i++) {
                items[i - head] = items[i];
            }
            tail -= head;
            head = 0;
        }
    
        items[tail] = item;
        tail++;
        returntrue;
    }

    publicString dequeue() {
        // 队列已空
if(head == tail) {
            returnnull;
        }
        String ret = items[head];
        head++;
        returnret;
    }
}

循环队列（实现一）

tail位置不存储数据，队空的条件是tail==head，队满的条件是(tail+1)%n=head

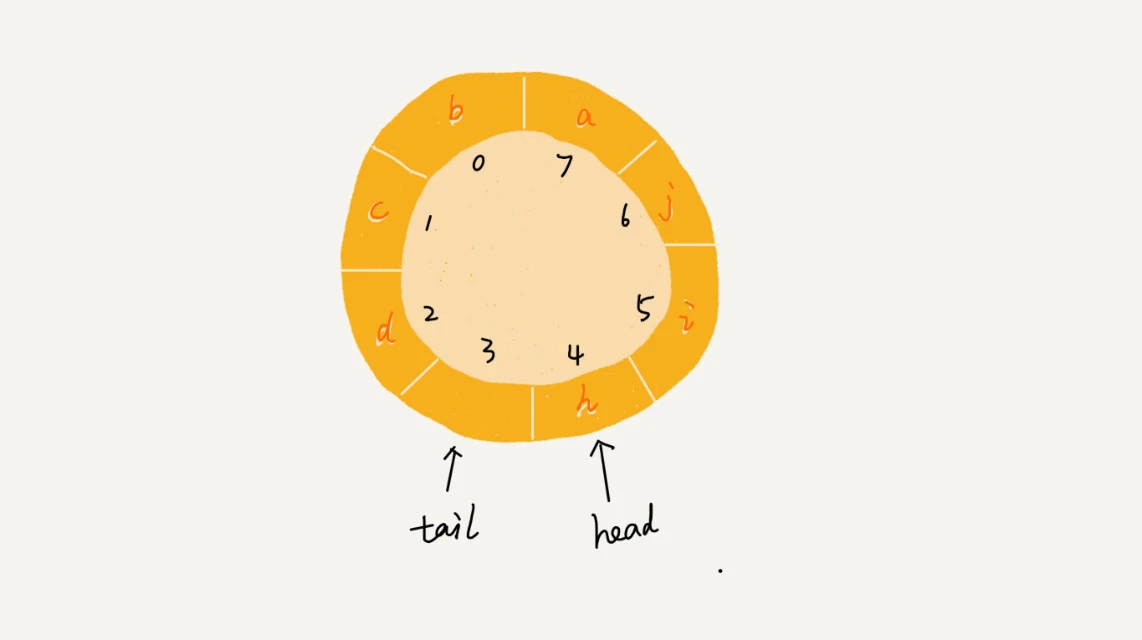
Java

publicclassCircularQueue {
    privateString[] items;
    privateintn = 0;
    privateinthead = 0;
    privateinttail = 0;

    publicCircularQueue(intcapacity) {
        items = newString[capacity];
        this.n = capacity;
    }

    publicbooleanenqueue(String item) {
        // 注意此种循环队列，tail位置不放元素，当tail的下一位是head的时候， 刚好就是队列满了
if((tail + 1) % n == head) {
            returnfalse;
        }

        items[tail] = item;
        // 注意循环队列，拿的是取模的下标， 而不是tail++
tail = (tail + 1) % n;
        returntrue;
    }

    publicString dequeue() {
        // 队列已空
if(head == tail) {
            returnnull;
        }
        String ret = items[head];
        // 注意循环队列，拿的是取模的下标， 而不是head++
head = (head + 1) % n;
        returnret;
    }
}

递归

递归需要满足三个条件
- 一个问题的解可以分解为几个子问题的解
- 这个问题和分解之后的子问题，除了数据规模不同，求解思路完全一样
- 存在递归终止条件
如何编写递归代码，写出递归公式，找到终止条件
- 编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

Java

假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？

把所有走法分为两类，第一类是第一步走了 1 个台阶，另一类是第一步走了 2 个台阶。所以 n 个台阶的走法就等于先走 1 阶后，n-1 个台阶的走法 加上先走 2 阶后，n-2 个台阶的走法
所以递归公式：f(n) = f(n-1)+f(n-2)

终止条件，当只有一个台阶，f(1)=1；当n=2 时，f(2)=f(1)+f(0)。如果递归终止条件只有一个 f(1)=1，那 f(2) 就无法求解了
因此增加终止条件f(0)=1，优化下，增加条件f(2)=2

最终代码：
int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  return f(n-1) + f(n-2);
}

递归的问题
- 警惕堆栈溢出，可以通过在代码中限制递归调用的最大深度
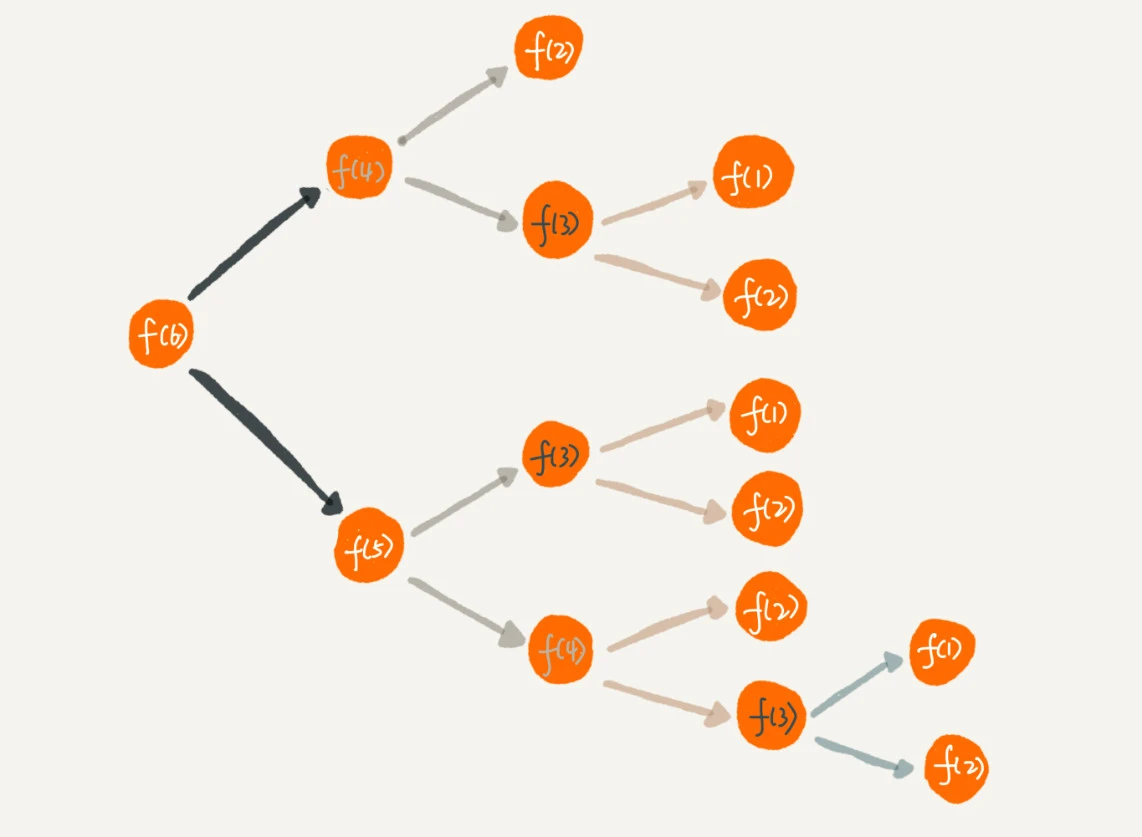
Java
```
// 全局变量，表示递归的深度。
int depth = 0;

int f(int n) {
  ++depth；
  if (depth > 1000) throw exception;

  if (n == 1) return 1;
  return f(n-1) + 1;
}
```
- 警惕重复计算
  - 想要计算 f(5)，需要先计算 f(4) 和 f(3)，而计算 f(4) 还需要计算 f(3)，因此，f(3) 就被计算了很多次
  - 可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)

Java

public int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;

// hasSolvedList可以理解成一个Map，key是n，value是f(n)
if (hasSolvedList.containsKey(n)) {
    return hasSolvedList.get(n);
}

int ret = f(n-1) + f(n-2);
hasSolvedList.put(n, ret);
return ret;
}

- 在空间复杂度上，因为递归调用一次就会在内存栈中保存一次现场数据，所以在分析递归代码空间复杂度时，需要额外考虑这部分的开销，比如我们前面讲到的电影院递归代码，空间复杂度并不是 O(1)，而是 O(n)

栈、队列和递归 ​

栈 ​

队列 ​

用数组实现的队列 ​

循环队列（实现一） ​

递归 ​

栈、队列和递归

栈

队列

用数组实现的队列

循环队列（实现一）

递归