跳表

• 概念：链表加多级索引=跳表

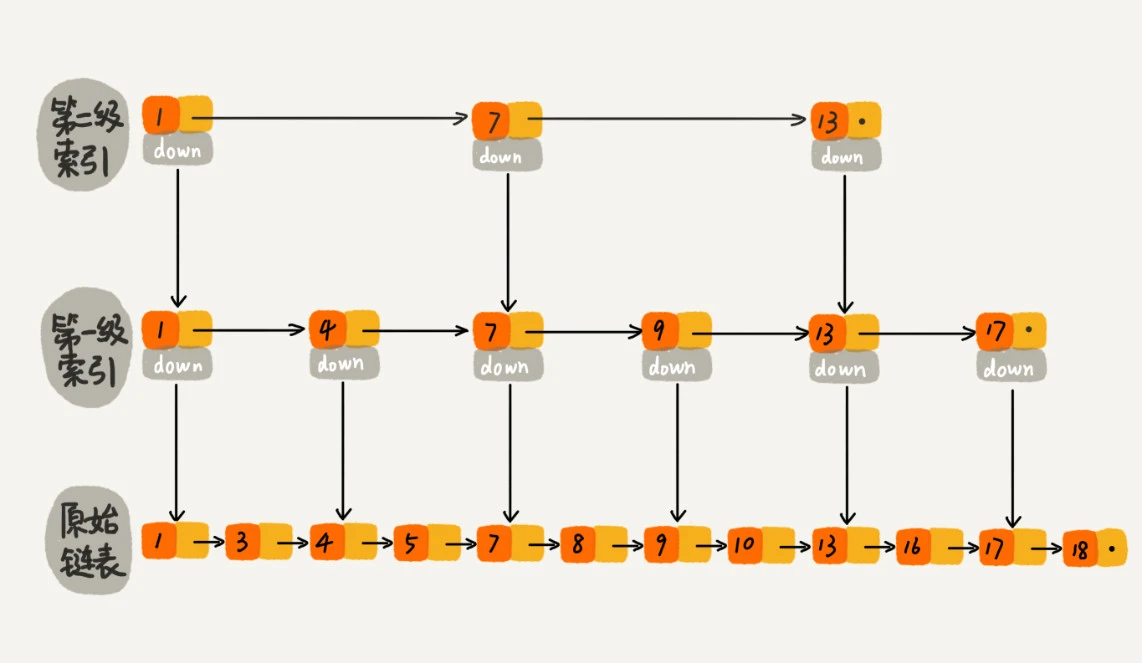
• 查询时间复杂度为**

  $$ O(logn) $$

  **

  • 假设每两个节点往上抽出一个节点，那第一级的节点数为n/2，第二级为n/4，第k级为**

    $$ n/(2^k) $$

    ; 假设共有h级，最高级的索引有2个节点，可得

    $$ n/(2^h)=2, h=log_2n-1 $$

    , 在加上原始链表这一层，整个跳表高度为

    $$ log_2n $$

    **, 若每一层要便利m个节点，那再跳表中查询一个数据的时间复杂度为O(m*logn)

  • 按上面这种结构，m最多为3, 如下图演示， 因此在跳表中查询任意数据的时间复杂度就是 O(logn)

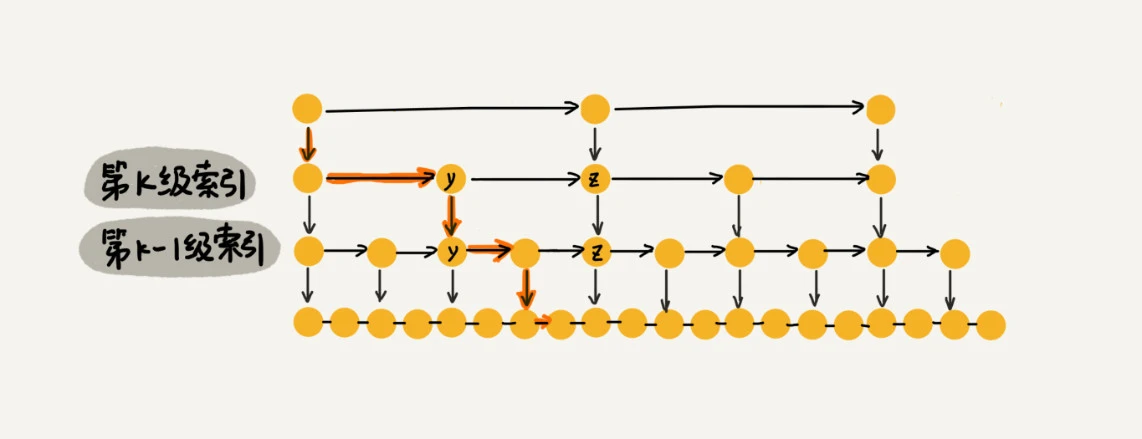
• 空间复杂度为O(logn)

  • 这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)
  • 假设每3个节点抽一个结点建立索引，总的索引结点大约就是 n/3+n/9+n/27+...+9+3+1=n/2。尽管空间复杂度还是 O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结点存储空间。

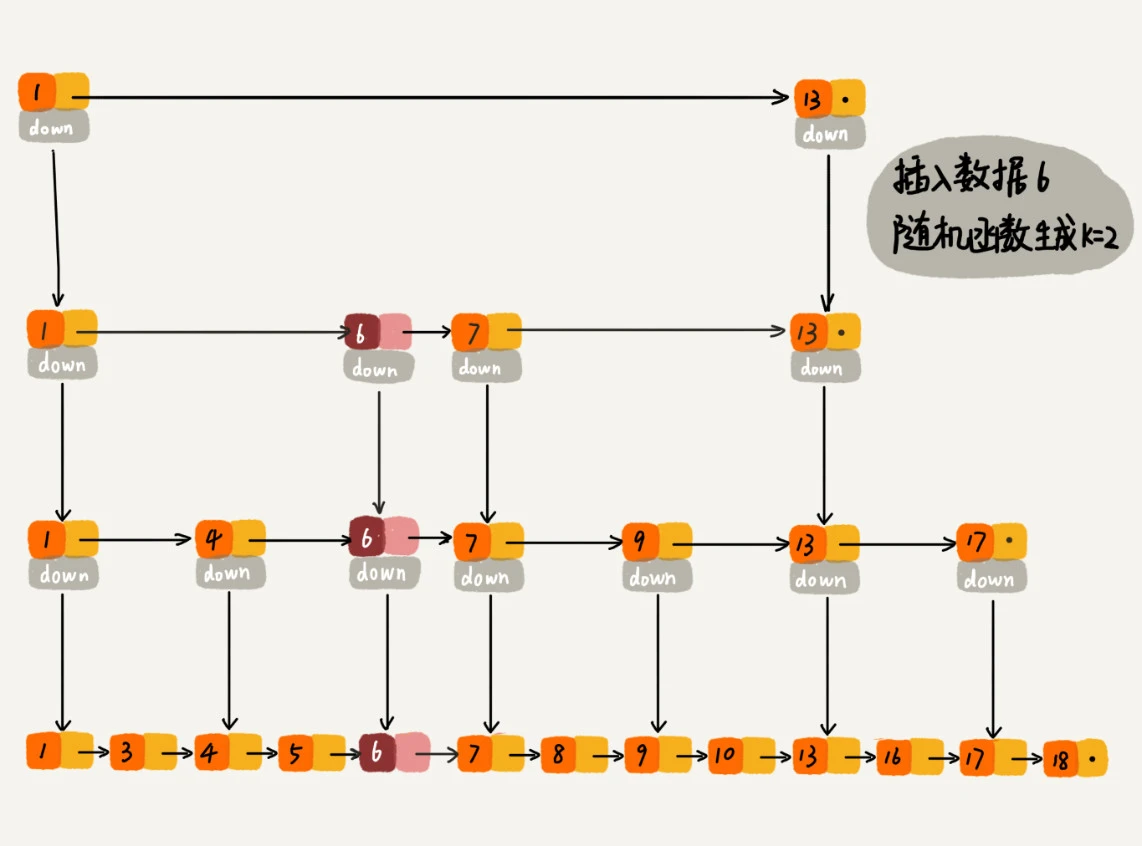
• 插入、删除操作的时间复杂度也是 O(logn)

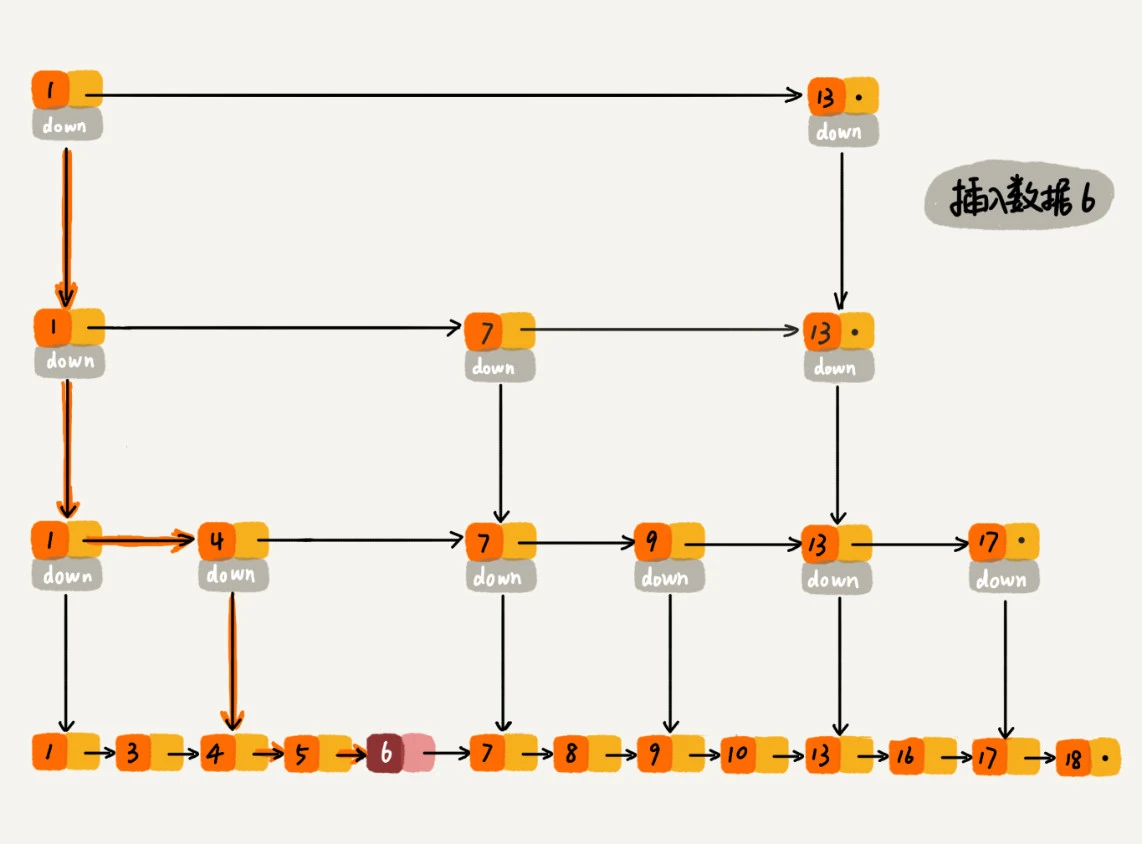
• 跳表索引动态更新， 通过随机函数来维护前面提到的“平衡性”， 比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中
  • 随机函数的选择很有讲究，从概率上来讲，能够保证跳表的索引大小和数据大小平衡性，不至于性能过度退化。