堆和堆排序

堆

堆是一种特殊的树:

• 堆是一个完全二叉树, 除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列。
• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。
  • 最小堆: 每个节点的值都小于或等于其子节点的值, 根节点总是最小的元素
  • 最大堆: 每个节点的值都大于或等于其子节点的值, 根节点总是最大的元素

堆排序

堆排序是一种原地的、时间复杂度为 O(nlogn) 的排序算法。

Topk问题

java中的PriorityQueue默认是最小堆, 堆结构与优先级队列非常相似, 从优先级队列中取优先级最高的元素, 相当于取出堆顶元素

• 从10万个数中找到前10大的数, 利用最小堆, 其堆顶元素是最小的, 往堆中塞k个元素, 使第k+n个元素与堆顶元素/最小的元素进行比较, 大则替换, 这样堆中就是前Topk元素了

/**
 * 从10万个数中找到前10大的数
 *
 * @authorxinzhang
 * @Description
* @create2025-01-10 19:58
 */
publicclassTopKComparison {

    publicstaticvoidmain(String[] args) {
        // 示例：生成10万个随机数
	int[] nums = newint[100000];
        for(inti = 0; i < nums.length; i++) {
            nums[i] = (int) (Math.random() * 1000000); // 随机生成0到999999的数
}

        intk = 10;
        int[] topK = findTopK(nums, k);

        // 输出结果
	System.out.println("前 " + k + " 大的数是：");
        for(intnum : topK) {
            System.out.println(num);
        }
    }

    /**
     * 最小堆排序
     * 时间复杂度为O(nlogk)，每次插入或删除堆的操作时间复杂度为O(log k)。总共需要遍历n个数
     * 空间复杂度为O(k)
     *
     * @param nums
* @param k
* @return
*/
private static int[] findTopK(int[] nums, intk) {
        // 最小堆，每次取出的都是最小的元素
	PriorityQueue<Integer> minHeap = newPriorityQueue<>();
        // 遍历数组
	for(intnum : nums) {
            if(minHeap.size() < k) {
                // 如果堆的大小小于k，直接插入
		minHeap.offer(num);
            } elseif(num > minHeap.peek()) {
                // 如果当前数大于堆顶元素，移除堆顶元素并插入当前数
		minHeap.poll();
                minHeap.offer(num);
            }
        }

        // 将堆中的元素转换为数组
	int[] result = newint[k];
        for(inti = 0; i < k; i++) {
            result[i] = minHeap.poll();
        }

        returnresult;
    }
}

高性能定时器

假设有一个定时器, 维护了很多定时任务, 每个任务都设定了一个要出发执行的时间点

• 如果定时器每过一个很小的单位时间, 就扫描一遍任务, 很耗性能
• 可以用优先级队列来解决。我们按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。

Top百分比问题

在动态数据中, 如何快速求中位数, 或是99%位置, 比如99%耗时

中位数

• 求中位数时, 先将存量数据前n/2存在大顶堆中, 后n/2存在小顶堆中, 那大顶堆的堆顶就是中位数

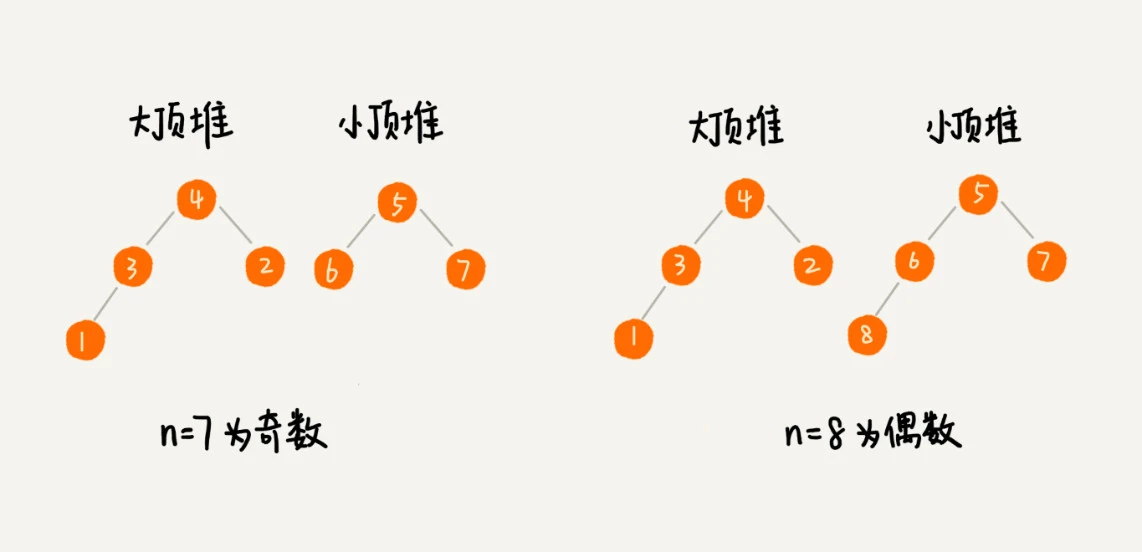
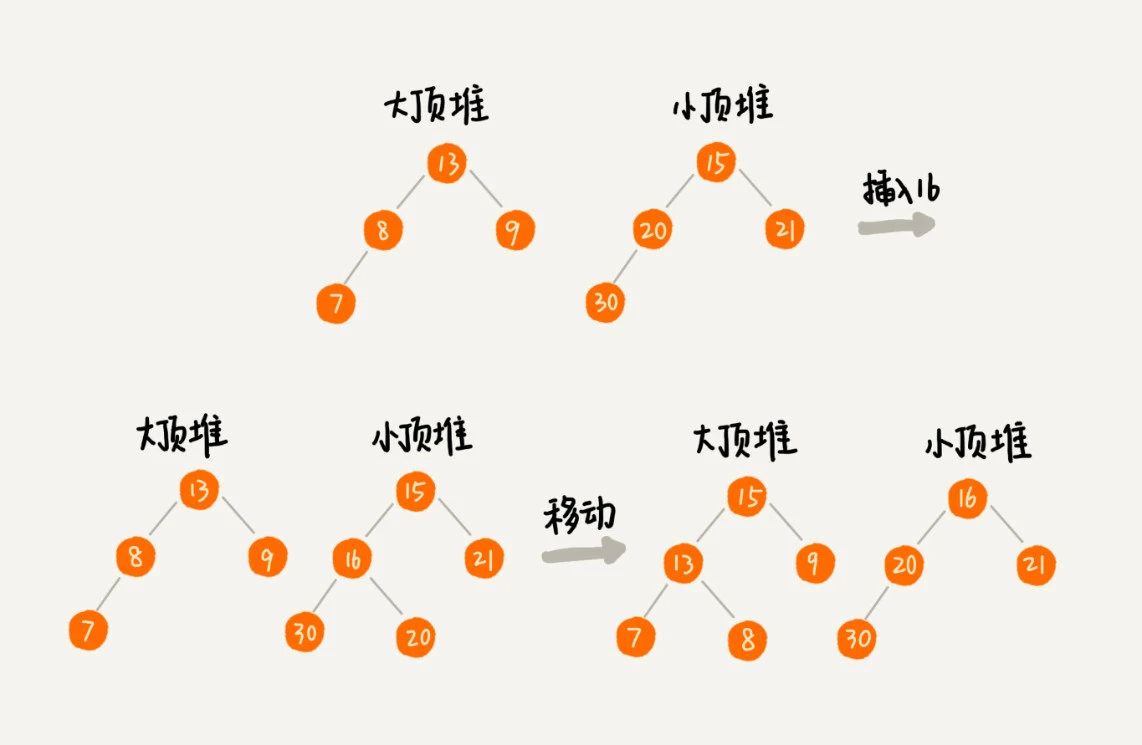
• 然后新增数据时, 如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；否则，我们就将这个新数据插入到小顶堆。同时, 将堆顶元素移动到另一个堆, 以平衡元素个数

百分比位置

• 跟中位数的算法类似, 先将存量数据前99%放在大顶堆, 后1%放在小顶堆, 然后每次新增数据后, 再判断下大小顶堆的数据个数是否满足比例要求, 如果不满足, 再移动堆顶元素进行平衡即可