线性排序

桶排序

• 原理: 将要排序的数据分到几个有序的桶里, 每个桶里的数据再单独进行排序, 桶内排完序后, 再把每个桶里的数据按照顺序依次取出, 组成的序列就是有序的了

• 时间复杂度为O(n), 简单想, 当桶的个数m尽可能趋近于n时, 只需分好桶再将桶合并即可; 最坏时间复杂度为**

  $$ O(nlogn) $$

  , 当桶个数最小=1, 也就是不分桶, 使用快排排序, 也就是

  $$ O(nlogn) $$

  **

• 适合用在外部排序(数据量比较大, 无法一次性加载到内存)中

  • 数据要能被划分桶

  • 数据在桶之间的分布比较均匀, 如果都分到一个桶, 时间复杂度也会退化到**

    $$ O(nlogn) $$

    **

• 示例: 排序订单

  • 先扫描得到最小金额, 最大金额
  • 再将订单根据金额分桶, 比如第一个桶1到1000金额的订单, 第二个桶存储1001到2000金额的订单, 依次类推
  • 再将每个桶中的订单排序, 最后将桶依次合并
  • 

计数排序

• 原理: 计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间
• 时间复杂度是O(n), 只涉及扫描遍历
• 适用于数据范围不大的场景, 且智能给非负整数排序, 若排序数据是其他类型, 需要在不改变相对大小的情况下, 转化为非负整数
• 示例: 如果你所在的省有 50 万考生，如何通过成绩快速排序得出名次呢？
  • 考生的满分是 900 分，最小是 0 分，这个数据的范围很小，所以我们可以分成 901 个桶，对应分数从 0 分到 900 分。根据考生的成绩，我们将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生，所以并不需要再进行排序。我们只需要依次扫描每个桶，将桶内的考生依次输出到一个数组中，就实现了 50 万考生的排序
• 最后桶合并的过程, 可以从前往后合并, 但就不是稳定排序了, 为保证稳定, 可以从后往前, 出栈思维
  • 示例: 假设只有 8 个考生，分数在 0 到 5 分之间。这 8 个考生的成绩我们放在一个数组 A[8]中，它们分别是：2，5，3，0，2，3，0，3
  • 考生的成绩从 0 到 5 分，我们使用大小为 6 的数组 C[6]表示桶，其中下标对应分数, C[6]存储的是对应分数的考生个数

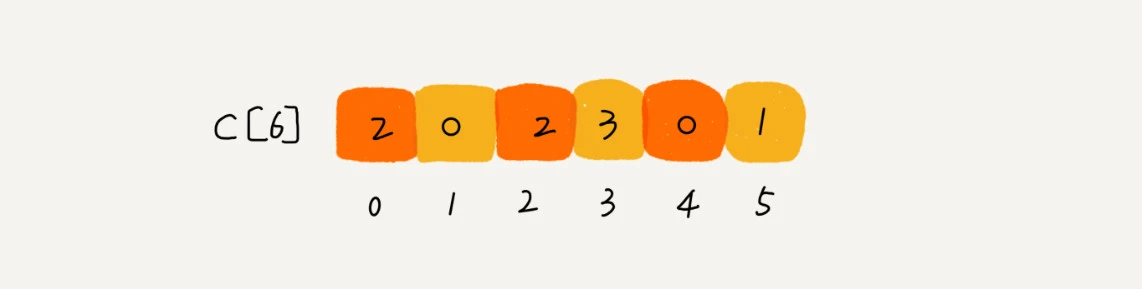
• 对C[6]顺序求和

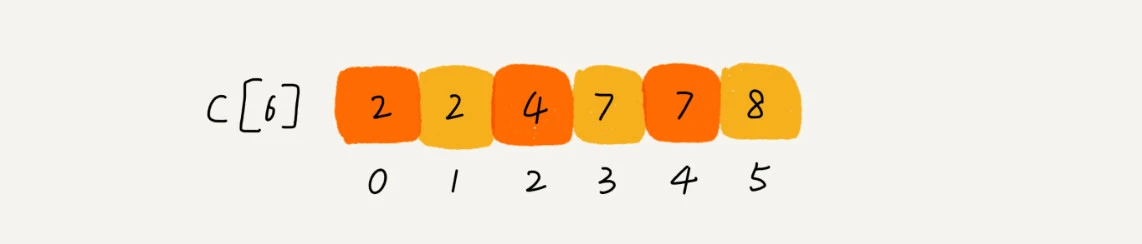
• R[8]存储最终有序的数组, 从后往前扫描数组A[8]
  • 扫描到3时, 从C[6]中拿到下标为3的值7, 那3应该在R数组中下标为6的位置(比3小的元素有7个), 同时3位置的值要-1变成6(已经取了一个元素)
  • 扫描到0时, C[0]=2, 也就是说在R数组中的下标为1, 同时C[0]的值要-1
  • 依次类推, 当A数组扫描完后, R数组就是有序的了

// 计数排序，a是数组，n是数组大小。假设数组中存储的都是非负整数。
public void countingSort(int[] a, int n) {
  if (n <= 1) return;

  // 查找数组中数据的范围
  int max = a[0];
  for (int i = 1; i < n; ++i) {
    if (max < a[i]) {
      max = a[i];
    }
  }

  int[] c = new int[max + 1]; // 申请一个计数数组c，下标大小[0,max]
  for (int i = 0; i <= max; ++i) {
    c[i] = 0;
  }

  // 计算每个元素的个数，放入c中
  for (int i = 0; i < n; ++i) {
    c[a[i]]++;
  }

  // 依次累加
  for (int i = 1; i <= max; ++i) {
    c[i] = c[i-1] + c[i];
  }

  // 临时数组r，存储排序之后的结果
  int[] r = new int[n];
  // 计算排序的关键步骤，有点难理解
  for (int i = n - 1; i >= 0; --i) {
    int index = c[a[i]]-1;
    r[index] = a[i];
    c[a[i]]--;
  }

  // 将结果拷贝给a数组
  for (int i = 0; i < n; ++i) {
    a[i] = r[i];
  }
}

• 补充: 看看非稳定排序的代码

public class CountingSort {
    /**
     * 计数排序
     *
     * @param arr 要排序的数组大小
     * @param n   数组元素个数
     */
    public static void sort(int[] arr, int n) {
        if (n <= 1) {
            return;
        }

        //默认数组最大的元素为数组第一个元素
        int max = arr[0];
        //遍历数组的所有的元素，找到最大的元素
        for (int i = 1; i < n; i++) {
            //若后面的元素大于指定的数组元素，则把元素进行交换
            if (arr[i] > max) {
                max = arr[i];
            }
        }

        //申请一个计数数组，下标从0~max。
        int[] c = new int[max + 1];

        //遍历数组，将每个元素的个数放入到计数数组中，比如分数为0的元素，在c[0]就累加1，依次类推
        for (int i = 0; i < n; i++) {
            c[arr[i]]++;
        }

        //开始重新整理c[]数组，将c[]数组顺序求和，比如分数0的个数1，分数为1的个数为3。那么重新整理后，分数<=0的为1，分数<=1人数诶1+3=4个，因为包含了<=0的个数，依次类推
        //所以终止条件为i<=max
        for (int i = 1; i <= max; i++) {
            c[i] = c[i] + c[i - 1];
        }

        //这时候开始进行排序，创建一个跟要排序的数组一样大小的数据空间
        int[] temp = new int[n];

        //开始循环需要排序的数据
        for (int i = 0; i < n; i++) {
            //计算出需要往temp临时数组哪个索引位置存放arr[i]的值。
            //根据原始数组的值找到计数数组的对应值的计数个数，得到c[arr[i]]的值，也就是temp数组从0开始，所以需要减一
            int index = c[arr[i]] - 1;
            temp[index] = arr[i];
            //每次循环，计数数组的元素值减一，因为数组放到了temp数组中
            c[arr[i]]--;
        }

        //重新赋值
        for (int i = 0; i < n; i++) {
            arr[i] = temp[i];
        }
    }
}

基数排序(Radix Sort)

• 原理: 利用稳定排序的思路, 先比较低位, 再比较高位
• 时间复杂度为O(n)
• 适用于可分隔出独立的"位"来比较的数据, 而且位之间有递进的关系, 且每一位的数据范围不能太大, 要可以用线性排序算法来排序
• 示例: 给 10 万个手机号码从小到大排序
  • 手机号码11位, 先按最后一位排序, 然后再按倒数第二位排序, 依次类推, 经过11次排序之后, 手机号码就有序了
  • 给每一位来排序, 可以使用上面的桶排序或计数排序

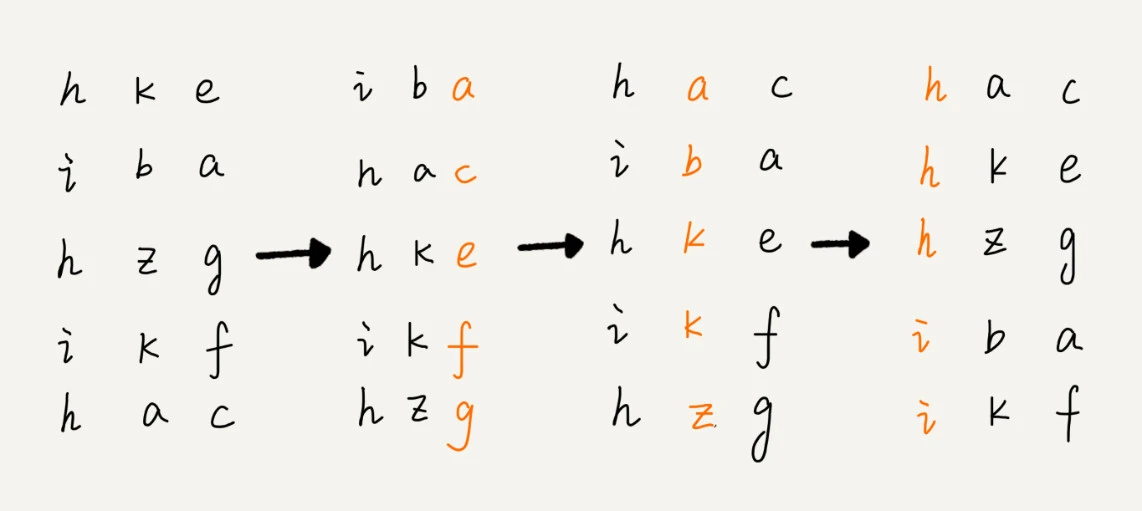
• 示例: 给牛津字典中的 20 万个英文单词排序
  • 单词长度不等长, 可以把所有的单词补齐到相同长度，位数不够的可以在后面补“0”，因为根据ASCII 值，所有字母都大于“0”，所以补“0”不会影响到原有的大小顺序, 这样就可以继续用基数排序了