树

相关概念

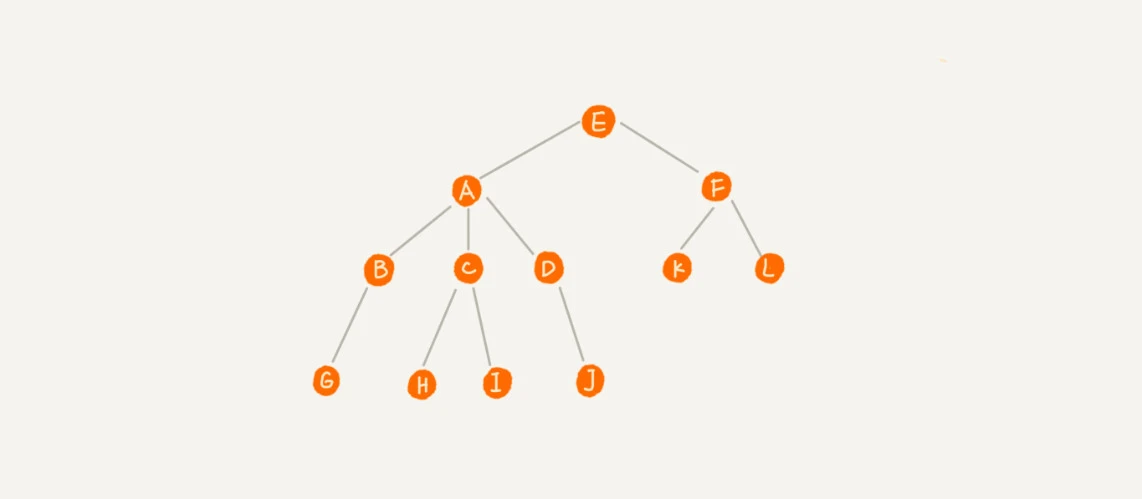
• 父节点, 子节点, 根节点, 兄弟节点, 叶/叶子节点

A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点，也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点

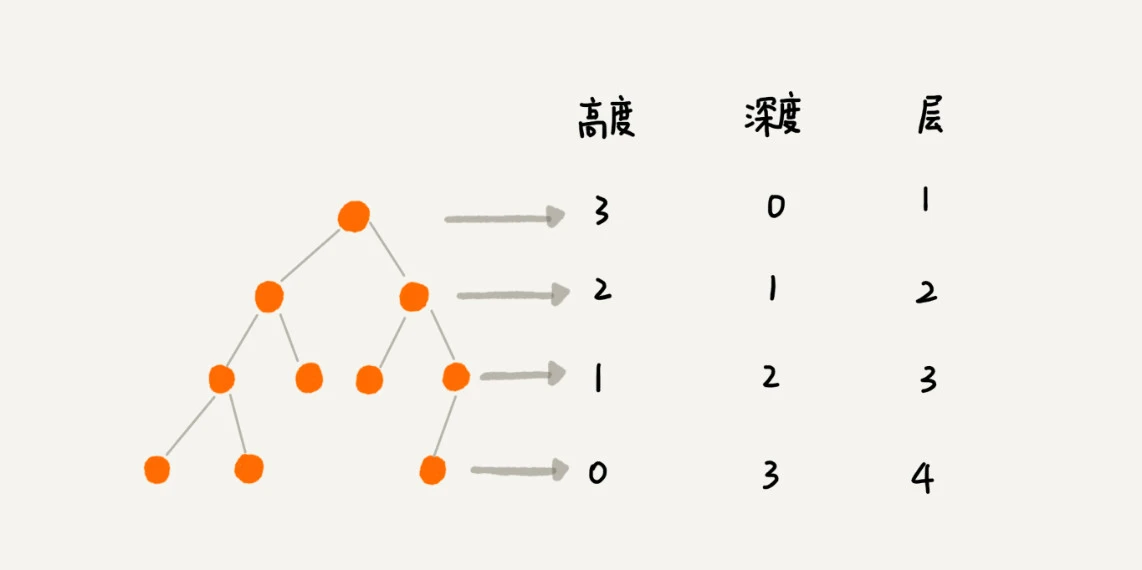
• 高度, 深度, 层

二叉树

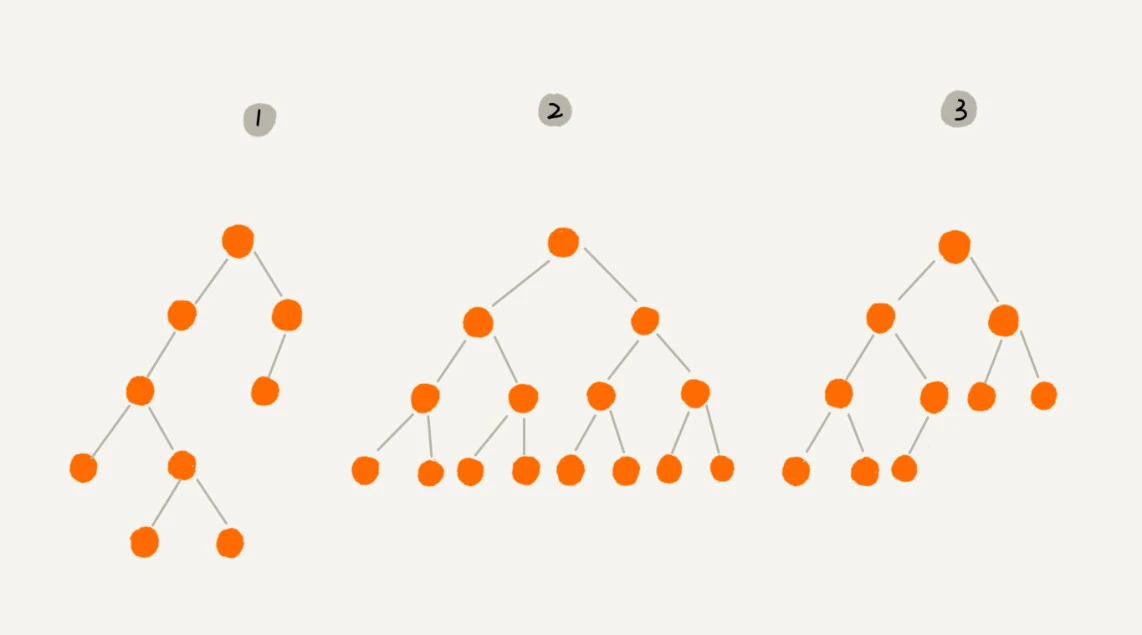
• 二叉树: 每个节点最多有两个子节点
• 满二叉树: 如图2, 叶子节点全在最底层, 除了叶子节点外, 每个节点都有2个子节点
• 完全二叉树: 如图3, 叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大

二叉树的存储

• 链式存储法

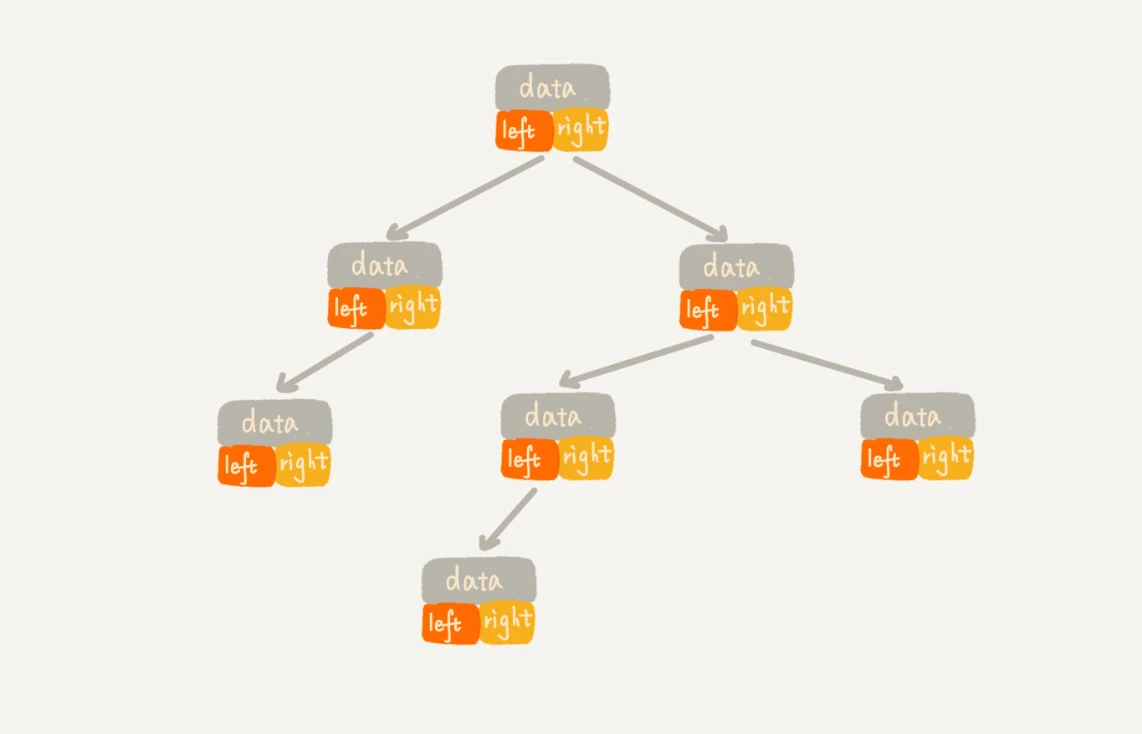
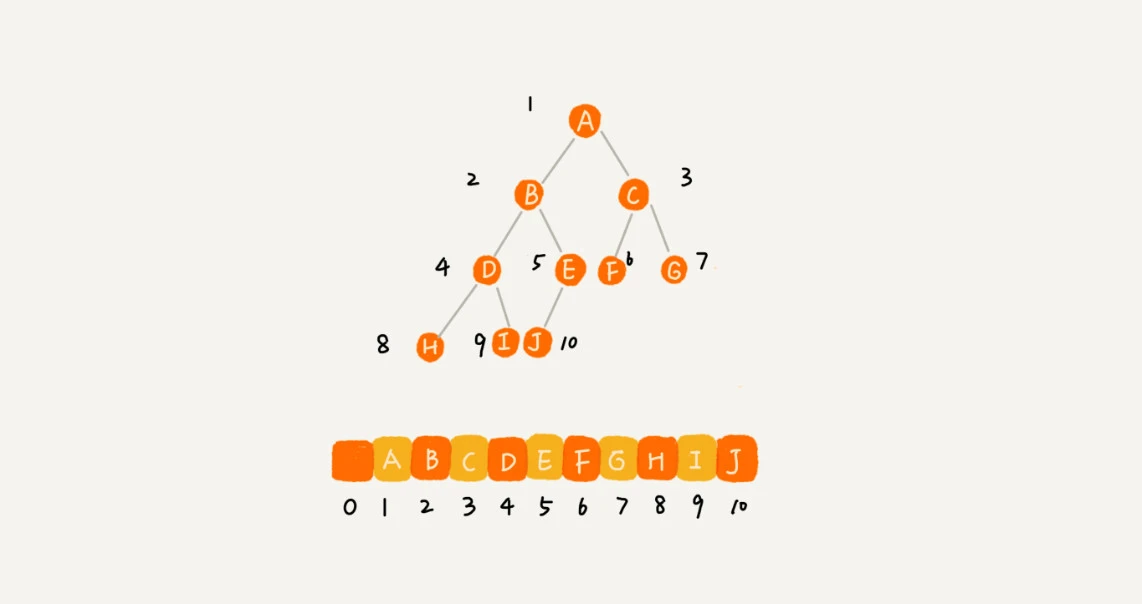
• 基于数组的顺序存储法, 把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
• 完全二叉树使用数组存储最节省内存, 如堆

二叉树的遍历

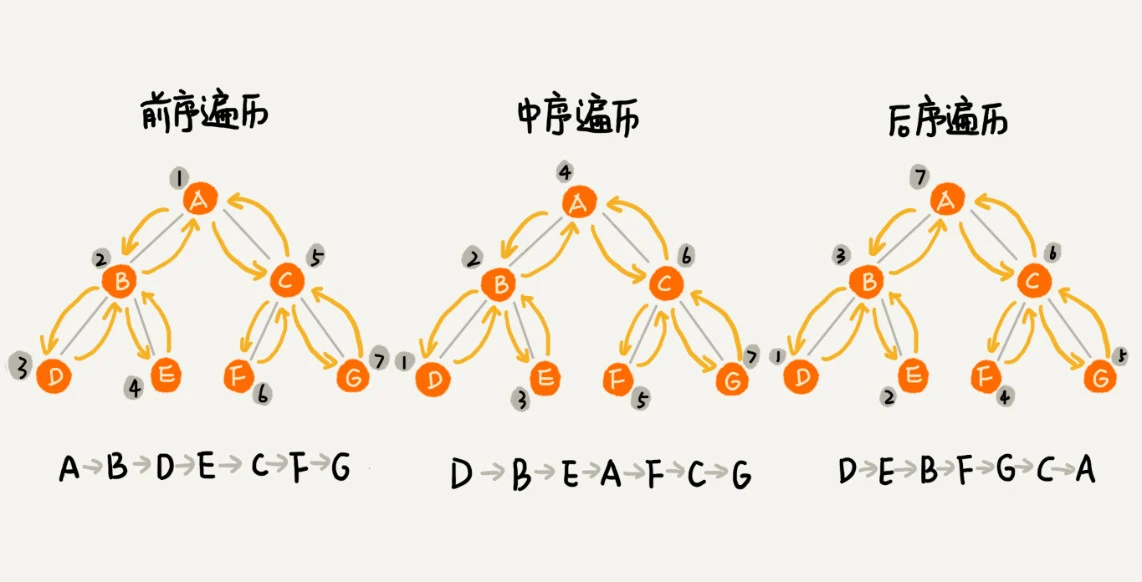
• 前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树
• 中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

• 递归过程, 伪代码如下, 由于每个节点最多遍历2次, 因此时间复杂度是O(n)

前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

二叉查找树

• 二叉查找树要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值
• 分析

  • 查找: 对比根节点, 相等则直接返回; 比根节点小, 则从左子树递归查找; 比根节点大, 则从右子树递归查找

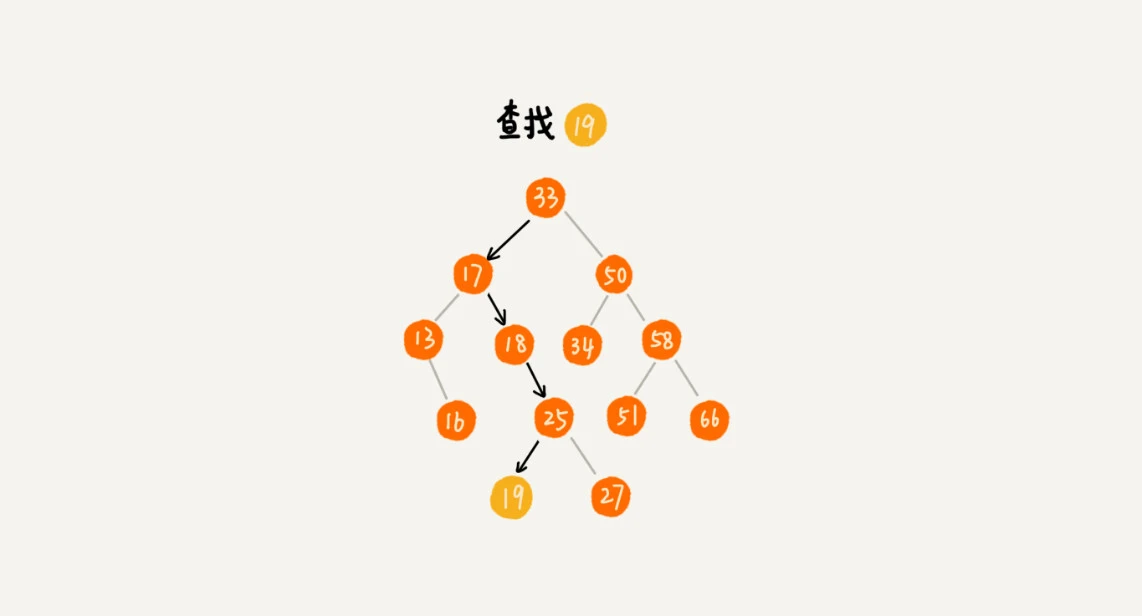
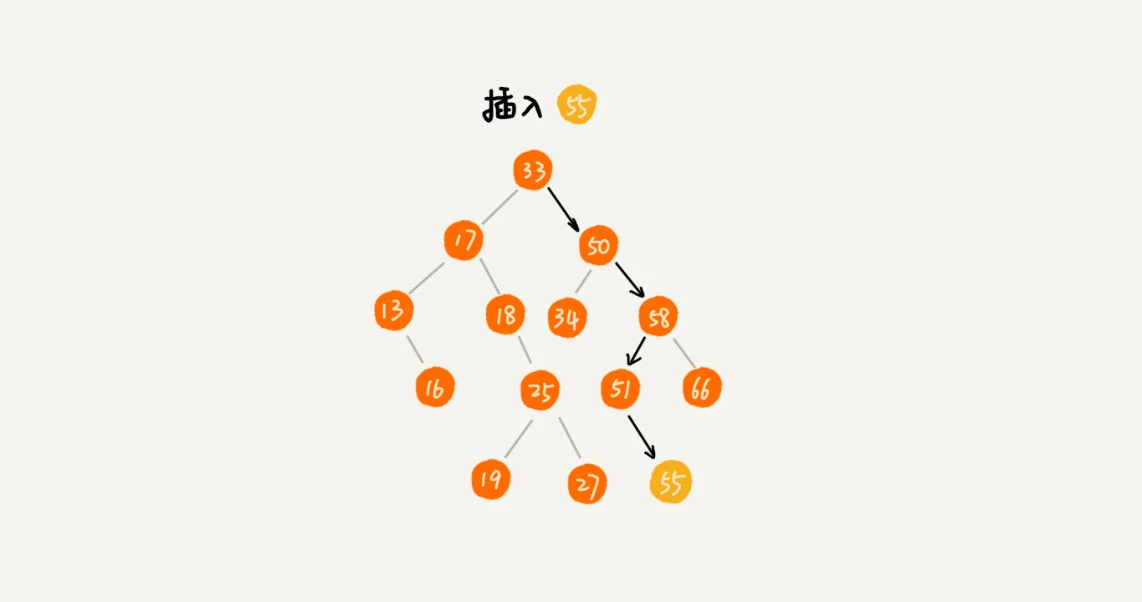
  • 插入: 一样对比根节点, 比根节点大, 若右子节点为空, 则直接插入, 否则在右子树中递归寻找插入位置; 同理, 比根节点小, 若左子节点为空, 则直接插入, 否则在左子树中递归寻找插入位置

  • 删除:

    • 若删除的节点没有子节点, 则直接将父节点对应指针指向null, 如下图55
    • 若删除的节点有一个子节点, 则需将父节点指向要删除的子节点的子节点, 如下图13
    • 若删除的节点有两个子节点, 则需找到父节点右子树下最小的节点, 替换到要删除的节点上, 再将这个最小节点删除, 如下图18

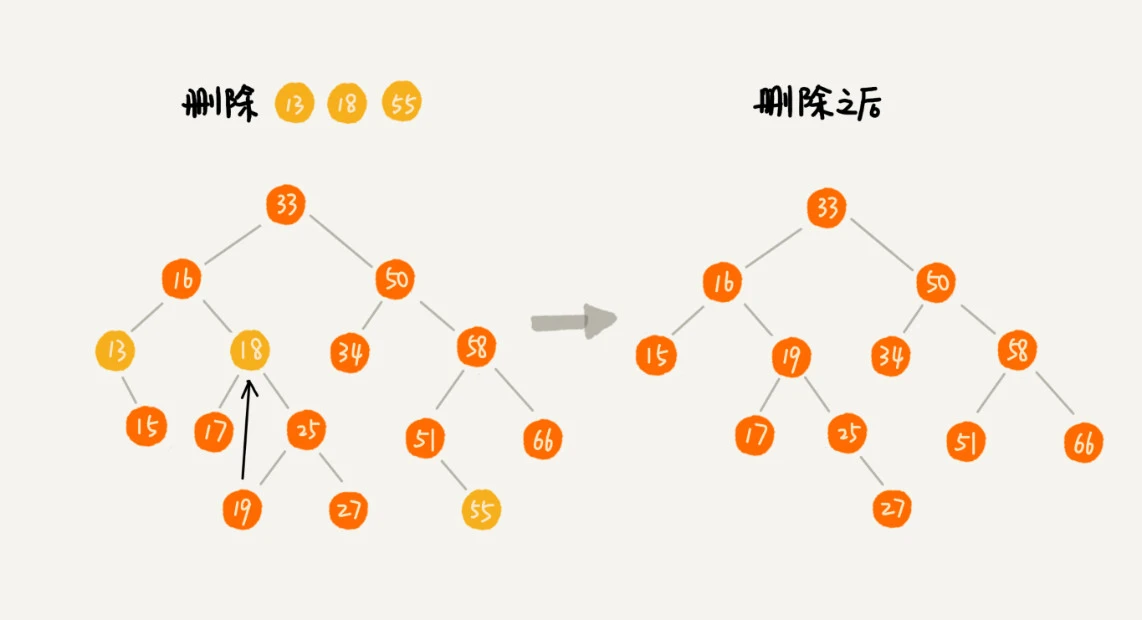
  • 中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是 O(n)，非常高效。因此，二叉查找树也叫作二叉排序树

• 支持重复数据的二叉查找树, 拓展方式有两种
  • 每个节点不仅存储一个数据, 通过链表或动态数据扩容
  • 插入时将相同的数据当做大于当前的数据处理, 那么在查找时, 遇到相同的值, 要在右子树中一直查找到叶子节点, 才能将所有相同的值都查出来
• 时间复杂度
  • 最糟糕的情况下退化成链表, 查找的时间复杂度是O(n)
  • 最理想的情况下是一个完全二叉树, 插入, 删除, 查找的时间复杂度是O(logn)

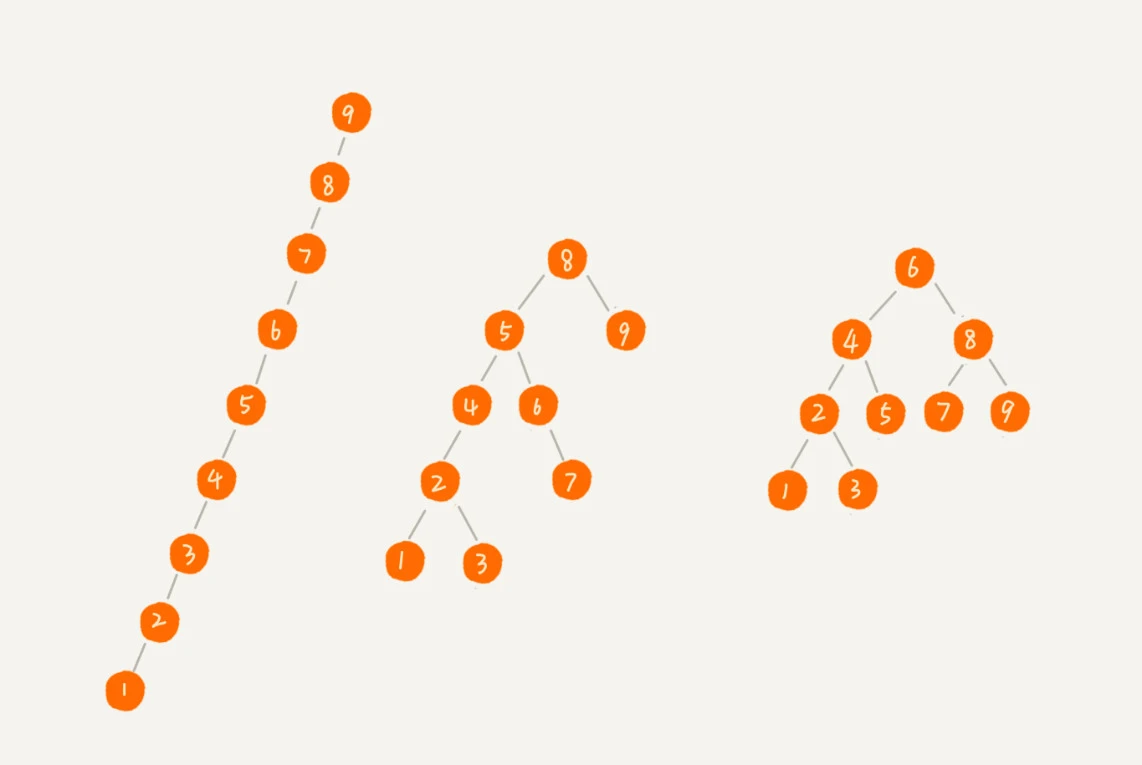
平衡二叉查找树

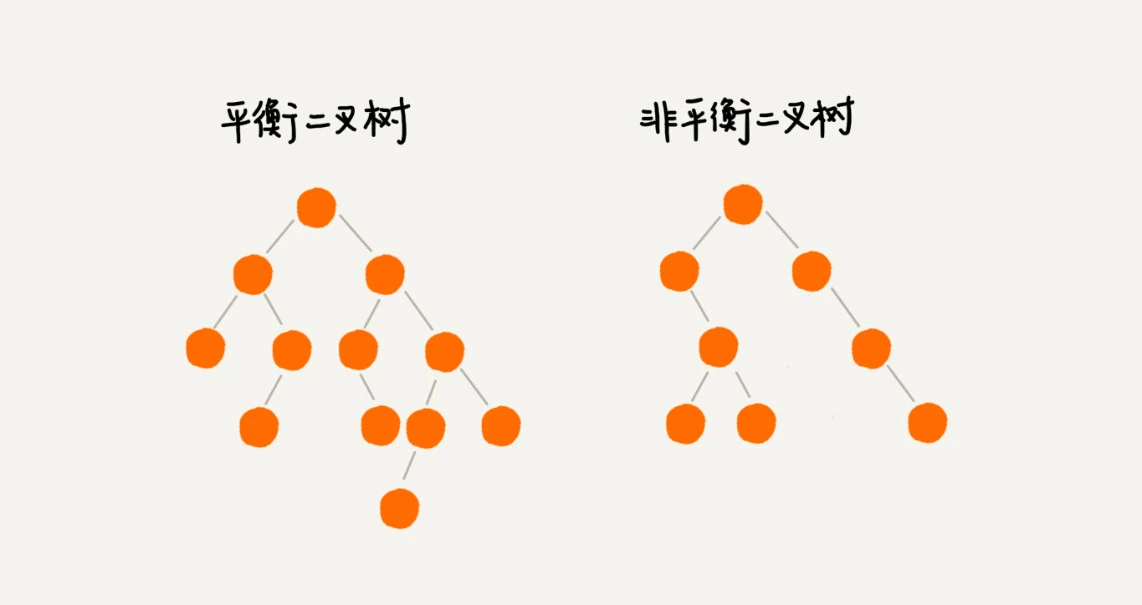
二叉树中任意一个节点的左右子树的高度相差不能大于 1。完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些

红黑树

红黑树的英文是“Red-Black Tree”，简称 R-B Tree。它是一种不严格的平衡二叉查找树

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

• 根节点是黑色的；
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

红黑树的优势:

• 做到了近似平衡，并不是严格的平衡，所以在维护平衡的成本上，要比 AVL 树要低。
• 插入、删除、查找各种操作性能都比较稳定

递归树

看不懂, 先放一边